Multi-Layer Perceptron

Gradient Descent

1. Initialize weights at random
2. Repeat
   • For each example in the training set:
     1. Predict $\hat{y}$ (forward pass)
     2. For each weight $w_{ij}$
        • Calculate derivate of error $\frac{dE}{dw_{ij}}$
        • Update weight $w_i^{(t)} = w_i^{(t-1)}-\alpha \frac{dE}{dw_{ij}}$
3. Until "done"
   • Fixed number of iterations
   • Error < error threshold
   • $w_i (t+1) - w_i(t)$ < change threshold

Back Propagation

Generalization of the Multi-layer Perceptron

• Number of inputs = number of attributes + bias
  • Input encoding can multiply the number of inputs
• Number of outputs = number of classes (classification) or 1 (regression)
• Error at output?
• Non-linear transformation
• Number of hidden layers
• Number of nodes per hidden layer
• Interconnection patterns
  • in feed-forward MLP, we assume fully interconnected

Try simple low layer neural networks, before high-layer neural nets.

Overfitting

In statistics, overfitting is the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit additional data or predict future observations reliably. An overfitted model is a statistical model that contains more parameters than can be justified by the data. The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e. the noise) as if that variation represented underlying model structure.

Problems & Solutions

• Too little training data
  • try to find ways of obtaining more data
  • think of model "transfer"
• Noisy data
  • preprocessing to eliminate outliers
  • Favor lower-complexity models
• Model complexity
  • Use regularization
  • Early stopping
  • Introduce drop-out (not tuning all weights all the time)

Regularization

To optimize the log loss error for logistic regression with an $L_2$ regularizer, minimize:

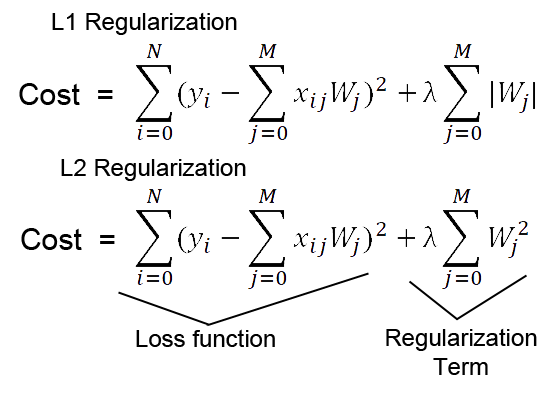
Early stopping

Determines a split for cross validation on when to stop training

Drop-Out

Randomly remove some weights during gradient descent. This adds a little bit of randomness.

Parameterization

import sklearn
sklearn.neural_network.MLPClassifier
# Parameters:
# - Stopping conditions for gradient descent
#     - max_iter
#     - n_iter_no_change
#     - tol
# - verbose 
# - warm_start  // transfer or previously learned weights
# - batch_size // size of batches for iterative learning
# - activation // non-linear function
# - alpha // L2 regularization
# - solver // (stochastic gradient descent) or lbgfs (variant using the hessian - 2nd derivative)
# - early_stopping // if early stopping, size of validation set
# - validation_fraction // what faction to use for validation for early stopping
# - hidden_layer_sizes // network architecture
# - learning_rate
# - learning_rate_init
# - momentum
# - random_state
# - shuffle

Explanable AI

Types of AI:

• Rule-based system
  • Modus Ponens
• Fuzzy logic
  • Fuzzy sets and modus Ponens
• Naive Bayes
  • Hypothesis testing
• Neural Network
  • Learned model with parameters X within 'package' Y