Synchronization

Loss of synchronization:

• in practice two data/digital signals are not equal. The result is that the timing of the receiver may slowly drift relative to the received signal.

Solution:

• data is sent in bit sequences called frames
• the receiving clock is started at the beginning of each bit sequence

Example:

• a frame consists of 11 bits
• assume that the synchronization at the start of the first bit is late at most 10% of $T_B$

Fulfill the following 2 conditions:

$(10+1/2) * T_S + 0.1 * T_B$ and $(10+1/2) * T_S > 10 * T_B$

These are satisfied if: $|\frac{T_S-T_B}{T_B}| < 3.8$

Asynchronous Transmission

• timing or synchronization must only be maintained within each character; the receiver has the opportunity to resynchronize at the beginning of each new character
• timing requirements are modest, sender and receiver are synchronized at the beginning of every character (8 bits if ASCII)
  • high overhead
  • overhead $= \mathrm{control_bits}/\mathrm{total_bits}$

Synchronization Transmission

• In this mode, blocks of characters or bits are transmitted. Each block begins with a preamble and ends with a postamble

• 2 types:

  • character-oriented
  • bit-oriented

• Character-oriented

  • the frame consists of a sequence of characters
  • SYN is a unique bit pattern that signals the receiver the beginning of a book
  • the receiver having detected the beginning of the block reads the information till it finds the postamble
  • the receiver having received the preamble, looks fo extra information regarding the length of the frame

• Bit oriented

  • in this mode, the frame treated as a sequence of bits. Neither data nor control information is interpreted in units of x-bit characters
  • a special bit pattern indicates the beginning of a frame
  • the receiver looks for the occurrence of the flag

Dealing with presence of errors

• Detect presence of errors (error detection)
• Try to correct them (error correction)
• If no correction have the mechanism to request retransmission (use of Automatic Repeat Request)

Random Errors

• An error occurs when a bit is altered between transmission and reception
• Random, statistically uniformly spread errors
  • occurrence of an error does not increase the probability that other bits, close to the one in error, while be in error
  • white noise is producing such errors
• For low BER and frames of "reasonable" length, most framers would experience no error or 1 error at most
  • example: BER = $10^6$ and length of frame = 8000 bits
  • probability of receiving a frame correctly > 0.992
  • probability of a frame having a single error = 0.007873
  • probability of having more than 1 error < 0.000127

Burst Errors

• occurrence of an error having occurred in the sequence, means bits preceding/following the one in error have higher probability than the average bit error probability to be in error
• error strings (clusters of error bits closely located in the sequence) form
• some channel related impairments producing error bursts
  • impulsive noise
  • "slow" fading/shadowing in wireless (relevance of bit rate to average time/distribution channel attenuation remains below certain level)
  • effect greater at higher data rates

Error detection and control

The objective is to detect and correct errors that occur in the transmission of frames.

Types of errors

• Lost frame
  • a frame that the receiver does not receive (e.g., because starting/clock extraction is not achieved due to excessive signal attenuation, increased levels of noise..)
• damaged frame
  • a frame that receiver receives, but some of its bits are in error

Error detection

• adds redundancy to transmitted message
• can deduce original despite some errors
• Example: block error correction code
  • map $k$ bit input onto an $n$ bit codeword
  • each distinctly different
  • if get error assume codeword sent was closest to that received
• means have reduced effective data rate
• most of the work concerning error correction & detection is making use of Galois field algebra

Code rate & minimum distance

Code rate $r$ = # of information bits in a block / # of total bits in a block = $k/n$.

The bandwidth expansion $1/r = n/k$.

The energy per channel bit $(E_c)$ is related to energy per information bit ($E_b$) through $E_c = rE_b$.

Minimum distance ($d_min$): minimum number of positions in which any 2 codewords differ.

Correctable and detectable errors

• A block code can correct at least $\mu$ errors if $d_{min} >= 2\mu +1$, $=> if d_{min}=3$, then $\mu = 1$. If there is only one error in the block, it can be corrected.
• A block code can detect any error pattern if the received $n$ bits do not correspond to a codeword.
• If there are $\lambda$ errors in the n-bits codeword, the existence of errors is detected with certainty if $\lambda < d_{min}$
• However, even when $\lambda >= d_{min}$, many of the corrupted blocks can still be detected
• Out of the $2^n$ possible $n$-bit combinations, only $2^k$ codewords can be generated, thus, there are $2^n-2^k=2^k(2^{n-k}-1)$ prohibited combinations
• Above statement applies when no error correction is used

Parity Check

• value of parity bit is such that character has even (even parity) or odd(odd parity number of ones)
• even number of bit errors goes undetected

Longitudinal Redundancy Checks

Cyclic Redundancy Check

• Based on cyclic error-correcting codes
• For a block of $k$-bits the transmitter generates $n$ bit sequence
• $n$ insert redundancy in the codeword
• Transmitter transmits the $k+n$ bits
• Receiver uses error detection process to decide if there were errors in the received sequence or otherwise.

Cyclic codes

• cyclic code is a block code, where the circular shifts of each codeword gives another codeword that belongs to the code
• they are error-correcting codes having algebraic properties that are convenient for efficient error correction & detection

Fundamentals CRC coding

• CRC codes treat bit strings as representations of polynomials with coefficients of 0 and 1 only (modulo 2 arithmetic)
  • $11001 = 1 * x^4 + 1*x^3+ 0*x^2 + 0* x^1 + 1*x^0 = x^4 + x^3 + 1$
• Polynomial arithmetic is done modulo 2
  • subtraction and addition are similar to XOR
  • division is similar to the one in decimal except the subtraction is done modulo 2
• Make sure you are familiar with mod2 arithmetic/algebra

Basic idea:

• the sender and receiver agree upon "a generator polynomial", $G(x)$, in advance
• the sender appends a checksum (corresponds to the $n$ redundancy bits) to the end of the (only data) frame, represented by the $M(x)$ polynomial, in a way that the polynomial $T(x)$, representing the {data + checksum bits} frame, is divisible by $G(x)$
• Upon receipt of the frame, the receiver (generates and) divides $H(x)$ by $G(x)$ using mod 2 division
• $H(x)$ is the polynomial corresponding to the received sequence
• if there is a remainder, there has been transmission error

How to compute the checksum

• if $n-1$ is the degree of $G(x)$, then append $n$ zero to the low order end of the frame; the resulting frame corresponds to the polynomial $X^n M(x)$.
• Divide $G(x)$ into $X^n M(x)$ using mod 2 division
  • $\frac{X^n M(X)}{G(X)} \Rightarrow D(X); R(X)$
• $D(X)$: divisor; $R(X)$: remainder
  • $X^n M(X) = G(X) \otimes D(X) \oplus R(X)$
• Subtract the remainder from $X^n M(x)$ using mod 2 subtraction/addition
• The result is the checksumed frame's polynomial, T(x)
  • $T(x) = X^n M(X) \oplus R(X)$

CRC Error Detection

• let us assume that some transmission errors occur
• instead of receiving $T(x)$, the receiver will receive $H(x)= T(x) \oplus E(x)$.
• If there are k "1" bits in $E(x)$, then k bit errors have occurred (probably)
• the receiver computes $T(x) \oplus E(x) / G(x)=E(x)/G(x)$
• if $G(x)$ contains two or more terms, (i.e. $n>1$) all single errors will be detected
• single-bit error means $E(X) = X^{m-1}$, where $0 < m \leq n + k$

Single error

• $H(X) = T(X)\oplus E(X)$ where
  • $E(X) = 0$ if no bit errors occur
  • $E(X) = X^{m-1}$ if only the $m$-th bit of the $[k+n]$-bit long frame is reversed $(0 < m \leq n + k)$; the large the value of $m$ is, the more significant the location of the bit within the frame is)
• $E(X) = L(X) \otimes G(X) \oplus F(X)$
• $H(X) - T(X) \oplus E(X) - T(X) \oplus L(X) \otimes G(X) \oplus F(X)$
• $\frac{H(X)}{G(X)} = D(X) \oplus L(X) \oplus \frac{F(X)}{G(X)}$
• Error will be detected if $\frac{F(X)}{G(X)} \neq 0$
• For $m-1>=n$, $L(X) = X^{m-n-1}$ and $\frac{F(X)}{G(X)} = 0$ Error is not detected
• For $m-1<n$, $L(X) = 0$ and $\frac{F(X)}{G(X)} \neq 0$ Error is detected

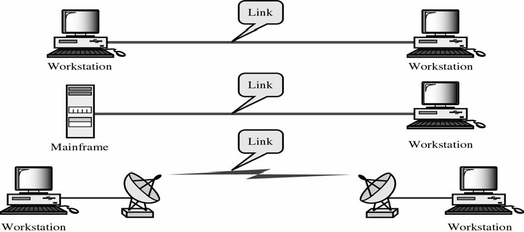
Line Configuration

• Topology
  • refers to physical arrangement of stations on the medium
  • two topologies are commonly used
    • point-to-point
    • multi-point

Point-to-point

• two stations
• traditionally mainframe computer and terminals
• between two routers / computers
• separate transmission line from the computer to each terminal
• the computer must have an I/O port for each terminal

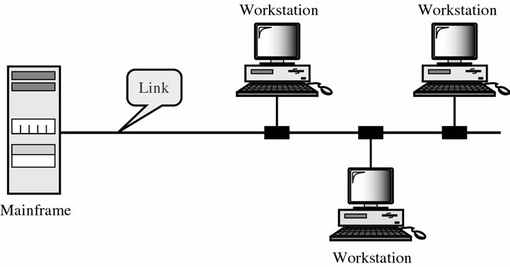
Multi-point

• typically, a local area network (LAN)
• a single "line" is needed
• the computer needs only single I/O port
  • eg. Ethernet, Token Ring, WiFi

Duplex

• classify data exchange as half or full Duplex
• half duplex (two-way alternate)
  • only one station may transmit at a time
  • requires one data path
• full duplex (two way simultaneous)
  • simultaneous transmission and reception between two stations
  • requires two data paths
    • separate media or frequencies used for each direction
  • or echo canceling