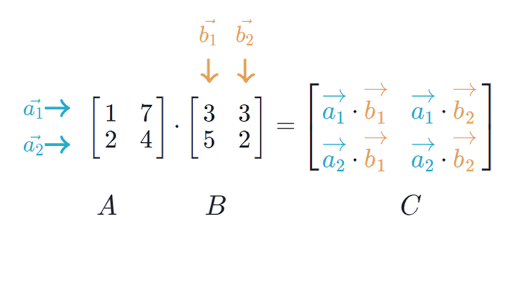Matrix Multiplication

Input: Two square matrices $A_{nxn}$ and $B_{nxn}$
Output: $AB$

# initialize matrix c (n x n)
for i in range (n):
    for j in range(n):
        c[i][j] = 0
        for k in range (n):
            c[i]c[j] = c[i][j] + a[i][k] * b[k][j]
return c

$T(n) = \Theta (n^3)$

Strassen Algorithm

Input: Two square matrices $A=[A_{11} A_{12}, A_{21}, A_{22}]$ and $B=[B_{11} B_{12}, B_{21}, B_{22}]$

if (n == 1):
    C = A * B
else:
    m_1 = (A_11 + A_22) * (B_11 + B_22)
    m_2 = (A_21 + A_22) * B_11
    m_3 = A_11 * (B_12 - B_22)
    m_4 = A_22 * (B_21 - B_11)
    m_5 = (A_11 + A_12) * B_22
    m_6 = (A_21 - A_11) * (B_11 + B_12)
    m_7 = (A_12 - A_22) * (B_21 + B_22)
    C_11 = m_1 + m_4 - m_5 + m_7
    C_12 = m_3 + m_5
    C_21 = m_2 + m_4
    C_22 = m_1 - m_2 + m_3 + m6
return C

Time complexity $T(n) = \Theta (n^{2.8})$