A Constraint Satisfaction Problem is a characterized by:

• A set of variables $V_1, V_2, ..., V_n$
• Each variable $V_i$ has an associated domain $\D_{V_i}$ of possible values.
• There are hard constraints on various subsets of the variables which specify legal combinations of values for these variables.
• A solution to the CSP is an assignment of a value to each variable that satisfies all the constraints.

Hard and Soft constraints

• Given a set of variables, assign a value to each variable that either
  • satisfies some set of constraints: satisfiability problems = "hard constraints"
  • minimizes some cost function, where each assignment of values to variables has some cost: optimization problems = "soft constraints"
• Many problems are a mix of hard and soft constraints (called constrained optimization problems).

Examples of Satisfiability:

• scheduling without preferences
• scheduling with preferences
• knapsack problem

Example of Optimization:

• scheduling with preferences
• knapsack
• TSP

Satisfiability

Generate-and-Test algorithm

• Generate all possibilities and test all (brute force)
• Generate the assignment space $D = D_{V_1} \cdot D_{V_2} \cdot ... \cdot D_{V_n}$
• Test cases become to big is a downside

Arc consistency algorithms

• Idea: prune the domains as much as possible before selecting values from them.
• A variable is domain consistent if no value of the domain of the node is ruled impossible by any of the constraints.

Constraint Graph

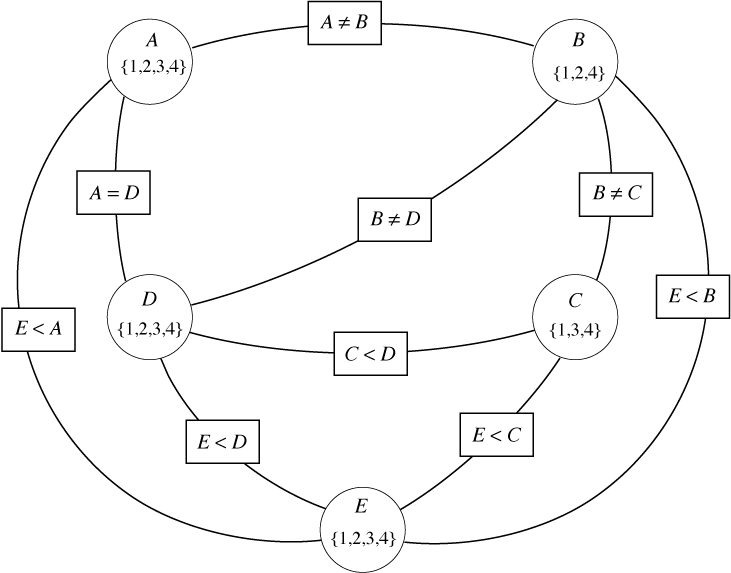
• oval shape for nodes representing variables
• rectangular shape for constraints
• there is a domain associated with each variable node
• there is an arc starting at the variable X for each constraint that involves it

AC-3 Algorithm

AC stands for arc consistency.

• Put all arcs in a Queue.
• Evaluate each arc to see if it is consistent.

G is a constraint network representing a CSP with V, D, C

Algorithm

Q = {(Vi, Vj) such that (Vi, Vj) is part of edges (G), i != j}
While Q not empty:
    Choose and remove (Vk, Vm) from Q
    If revise((Vk, Vm)) then:
        Q = Q union {(Vi, Vk) for all edges (G), i!= k, i!=m}
    End While
End Ac-3

Three possible results:

• At least one domain is empty -> no solution
• each domain is reduced to a single value -> unique solution
• certain domains have more than one value -> maybe none, maybe one, maybe multiple solutions, continue and explore

Greedy Search

• Greedy Search for planning
  • alphabetical order, small non-conflicting value
  • most constrained to least constrained domain
• Greedy search for knapsack
  • choose the highest value first. For two equal values, choose the least heavy
  • choose heaviest first. If two equal weights, choose hightest value
• Greedy search for TSP
  • go to closest city, if 2 equal choices, select in descending alphabetical order

Search Space

Local maximum (or minimum): There exists a better solution that cannot be reached by making local moves according to the cost function.

Global maximum (or minimum): Where the optimal solution is found. Where the cost function is minimized or maximized.

Plateau: An area of the search space which provides no clue as to where to go since all neighbors seem locally equal in their evaluation of the cost function.

Randomized Search

Random Restart

Algorithm for search with random restart

• we try to create a first complete solution
• we restart from the beginning with a new starting point

Random Step

Algorithm for search with random step

• we introduce random steps within the construction of a solution. Sometimes we take a path that is not locally the best.

Random Modification

ALgorithm for search with random modification

• we create a first complete solution
• we then modify parts of the solution following some random strategy

Generic algorithm:

• Starting with an initial (greedy) solution
• Repeat for N iterations:
  • Make local changes
  • If better (according to cost function):
    • Keep changes
  • Else
    • Keep change (according to some probability)

Simulated Annealing

• a well-known random modification algorithm

Simulated annealing is inspired by the process of restructuring an internal configuration of a solid which is annealed (e.g. crystallization process).

The solid heated up to melting point, so that its particles are randomly distributed. The material is then slowly cooled down, so that the particles reorganize in order to reach a low energy state.

How to Evaluate?

If we introduce random in the algorithm, we must repeat it many times to measure an average of its performance.

The performance could be in terms of runtime and/or quality of the obtained solution(s).

Population-based algorithms

Idea: Instead of exploring one solution at atime, explore M solution in parallel. The solutions are the individuals, and the set of M solutions is the population.

Examples

Known population-based algorithms:

• bee colony
• ant colony
• genetic algorithm

Algorithms inspired from social behavior or nature's behavior

• Particle swarm optimization (social behavior in flocking birds)
• Rain algorithm

Algorithm

• Generate a population $X(t)$ of $M$ individuals
• Repeat
  • Perform variations on individuals to generate new individuals
  • Evaluate individuals and retain the "best" $M$ to generate population $X(t + 1)$
• Until stopping condition

Generic Algorithm

• Generate a population $X(t)$ of $M$ individuals
• Repeat
  • Perform variations on individuals to generate new individuals
  • Evaluate individuals and retain the "best" $M$ to generate population $X(t + 1)$
• Until stopping condition
  1. Max $Nb$ iterations
  2. No better solution within K iterations
  3. One solution better than threshold on cost function

Genetic Algorithm

Algorithm inspired from genetic, including crossovers and mutations of ADN occurring during reproduction. The best adapted (according to a cost function) “parent” population will hopefully create even more adapted “children” individuals.

• Crossover: exchange portions from both parents

• Mutation: modify an element of an individual

• Generate a population X(t) of M individuals

• Repeat

  • Choose pairs of individuals (parents) using a measure to choose the most "fitted" individuals
  • For each pair, carry out cross-overs by exchanging part of solutions from the parents to generate children
  • Generate some children as « copies » of a parent
  • Make changes (mutations) to certain children
  • Evaluate individuals and retain the “best” M to generate population X(t + 1)

• Until stopping condition