Reasoning

• Deduction: Given the rule and the cause, deduce the effect
  • rule: all balls that come from bag W are white
  • deduction: here is a ball X from bag W, what color is X?
• Induction: Given a cause and an effect, induce a rule
  • rule is unknown, many observations find balls from bag W are white
  • induction: all balls that come from bag W must be white
• Abduction: Given a rule and an effect, abduce a cause
  • rule: all balls that come from bag W are white
  • abduction: here is a white ball, it must have come from bag W.

Reasoning in AI

Commonsense Reasoning

• spatial reasoning (e.g. on top, next to, under)
• temporal reasoning (e.g. yesterday, tomorrow)

Logic

• classical logic
  • propositional logic
  • predicate logic
• description logic
• fuzzy logic

Reasoning with certainty

• fuzzy logic
• probabilistic reasoning

Analogical reasoning

Classical Logic

Propositional Logic

A proposition corresponds to a statement. A statement is a declarative sentence which can be true(1) or false (0). Propositional logic is sometimes referred to as a sentinel logic or statement logic.

When propositions are written using the proper syntax, we can say that they are well-formed formulae (wff).

Tautology is a proposition that is always true. Contradiction is a proposition that is always false.

Predicate Logic

Adding onto propositional logic we can include

• functions, for ex. weather(Tuesday, rain)
• quantifiers (universal and existential), for ex. $\forall$X likes(X, ice_cream)
• connectives, for ex. ∀X ∀Y friends(X,Y) → likes(X,Y) ∧ likes(Y,X)

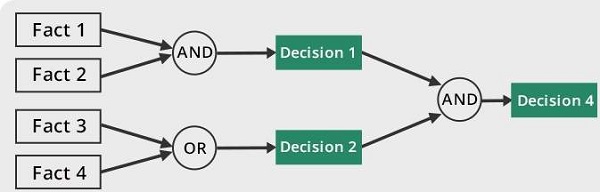
Rule-based Systems

Reasoning with inference engine

• forward chaining
  • 
• backward chaining
  • 

Require

• rules
• set of facts

Purpose

• Establish new facts (deduction)
• Show that certain facts are true based on what is already known.

Advantage over a database

• do not have to explicitly state everything
• can generalize and infer new knowledge

Discussion about Classical Logic

Closed vs. Open World

• in a closed world, everything unknown is false
• in an open world, everything is possible

Monotonic vs. Non-Monotonic

Monotonic:

• may not learn any knowledge that contradicts what it already knows
• never replaces a statement with its negation
• knowledge base only grows
• advantages
  • simplified true maintenance

Non-monotonic:

• learn knowledge that contradicts what it already knows
• replaces old knowledge with new
• advantages
  • increased applicability to real domains

Deduction / Induction

Deduction:

• Data + rules -> Output

Induction:

• Data + output -> rules

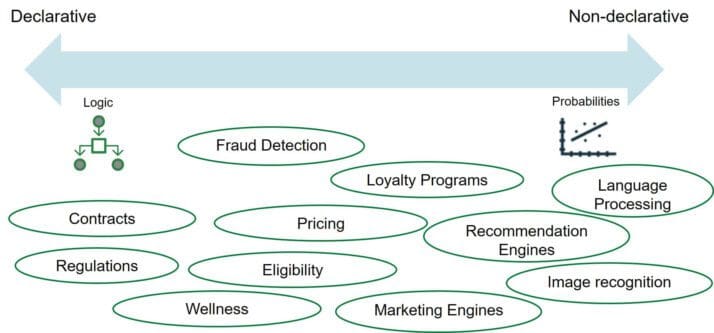
Positioning Logic in the AI Ecosystem

Fuzzy Logic

Fuzzy logic is an extension of Boolean logic created by Lotfi Zadeh in 1965 based on his mathematical theory of fuzzy sets, which is a generalization of classical set theory.

By introducing the notion of degree in the verification of a condition, thus allowing a condition to be in another state than true or false, the fuzzy logic confers a very appreciable flexibility on the reasoning that uses it, which makes possible taking into account inaccuracies and uncertainties.

One of the interests of fuzzy logic in formalizing human reasoning is that rules are stated in natural language.

Applications

• Help in decision making, and diagnostic
  • medical domain, professional orientation
• object recognition
• fuzzy control
  • braking Systems
  • elevators
• appliances control
  • washing machine, rice cookers
• audiovisual systems
  • auto-focus on camera
• car embedded systems
  • suspension, cooling

Linguistic Variables

A linguistic variable is represented by a triplet ($V$,$X_V$, $T_V$)

• $V$ : name of a variable (age, size, temperature, service quality, ...)
• $X_V$: set of possible values for $V$
• $T_V$: set of fuzzy subsets for $X_V$, used to characterize $V$

Fuzzy Operators

• min (A, B) = AND
• max (A, B) = OR
• 1-A = NOT

Reasoning in Fuzzy Logic

Architecture of Fuzzy System

Input -> Fuzzifier -> Inference Engine -> Defuzzifier -> Output

Adapted Modus Ponens

1. Recuperate the membership degrees of the antecedents
2. Combine the membership degrees of the antecedents using the fuzzy operators
3. Transfer the resulting membership degree on the consequence